Interpretation of the spectra of first-row transition metal complexes

Interpretation of the spectra of first-row transition metal complexes using Tanabe-Sugano diagrams

For ALL octahedral complexes, except high spin d⁵, simple CFT would predict that only 1 band should appear in the electronic spectrum and that the energy of this band should correspond to the absorption of energy equivalent to Δ. In practice, ignoring spin-forbidden lines, this is only observed for those ions with D free ion ground terms i.e., d¹, d⁹ as well as d⁴, d⁶.

The observation of 2 or 3 peaks in the electronic spectra of d², d³, d⁷ and d⁸ high spin octahedral complexes requires further treatment involving electron-electron interactions. Using the Russell-Saunders (LS) coupling scheme, these free ion configurations give rise to F free ion ground states which in octahedral and tetrahedral fields are split into terms designated by the symbols A_2(g), T_2(g) and T_1(g).

To derive the energies of these terms and the transition energies between them is beyond the needs of introductory level courses and is not covered in general textbooks[10,11]. A listing of some of them is given here as an Appendix. What is necessary is an understanding of how to use the diagrams, created to display the energy levels, in the interpretation of spectra.

In the laboratory component of the course we will measure the absorption spectra of some typical chromium(III) complexes and calculate the spectrochemical splitting factor, Δ. This corresponds to the energy found from the first transition below and as shown in Table 1 is generally between 15,000 cm^-1 (for weak field complexes) and 27,000 cm^-1 (for strong field complexes).

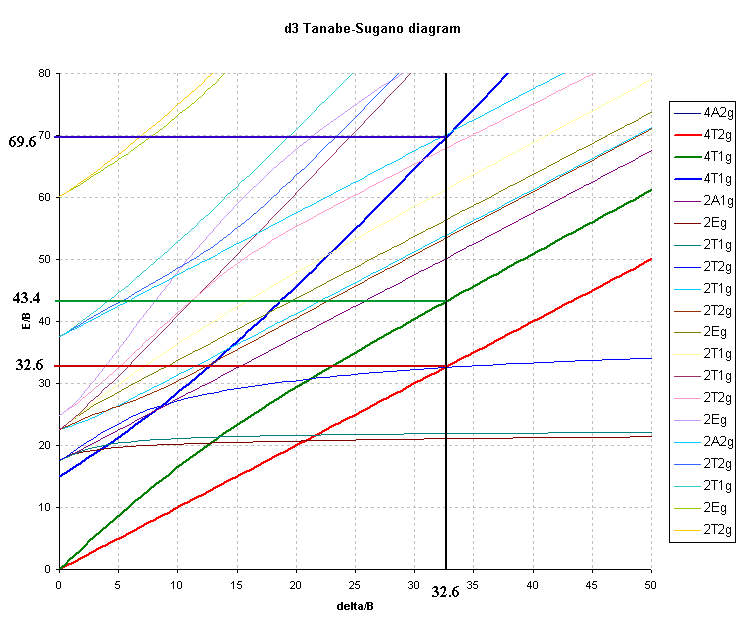
For the d³ octahedral case, 3 peaks can be predicted and these would correspond to the following transitions and energies:

⁴T_2g ← ⁴A_2g �� transition energy = Δ
⁴T_1g(F) ← ⁴A_2g �� transition energy = 9/5 * Δ - C.I.
⁴T_1g(P) ← ⁴A_2g �� transition energy = 6/5 * Δ + 15B' + C.I.

where C.I. is the configuration interaction arising from the "non-crossing rule".

Table 1. Peak positions for some octahedral Cr(III) complexes (in cm^-1).
Complex	ν1	ν2	ν3	ν2/ ν1	ν1/ ν2	Δ/B	Ref
Cr³⁺ in emerald	16260	23700	37740	1.46	0.686	20.4	13
K₂NaCrF₆	16050	23260	35460	1.45	0.690	21.4	13
[Cr(H₂O)₆]³⁺	17000	24000	37500	1.41	0.708	24.5	This work
Chrome alum	17400	24500	37800	1.36	0.710	29.2	4
[Cr(C₂O₄)₃]^3-	17544	23866	?	1.37	0.735	28.0	This work
[Cr(NCS)₆]^3-	17800	23800	?	1.34	0.748	31.1	4
[Cr(acac)₃]	17860	23800	?	1.33	0.752	31.5	This work
[Cr(NH₃)₆]³⁺	21550	28500	?	1.32	0.756	32.6	4
[Cr(en)₃]³⁺	21600	28500	?	1.32	0.758	33.0	4
[Cr(CN)₆]^3-	26700	32200	?	1.21	0.829	52.4	4

For octahedral Ni(II) complexes the transitions would be:

³T_2g ← ³A_2g �� transition energy = Δ
³T_1g(F) ← ³A_2g �� transition energy = 9/5 * Δ - C.I.
³T_1g(P) ← ³A_2g �� transition energy = 6/5 * Δ + 15B' + C.I.

where C.I. again is the configuration interaction and as before the first transition corresponds exactly to Δ.

For M(II) the size of Δ is much less than for M(III) and typical values for Ni(II) are 6500 to 13000 cm^-1 as shown in Table 2.

Table 2. Peak positions for some octahedral Ni(II) complexes (in cm^-1).
Complex	ν1	ν2	ν3	ν1	ν1/ ν2	Δ/B	Ref
NiBr₂	6800	11800	20600	1.74	0.576	5	13
[Ni(H₂O)₆]²⁺	8500	13800	25300	1.62	0.616	11.6	13
[Ni(gly)₃]^-	10100	16600	27600	1.64	0.608	10.6	13
[Ni(NH₃)₆]²⁺	10750	17500	28200	1.63	0.614	11.2	13
[Ni(en)₃]²⁺	11200	18350	29000	1.64	0.610	10.6	3
[Ni(bipy)₃]²⁺	12650	19200	?	1.52	0.659	17	3

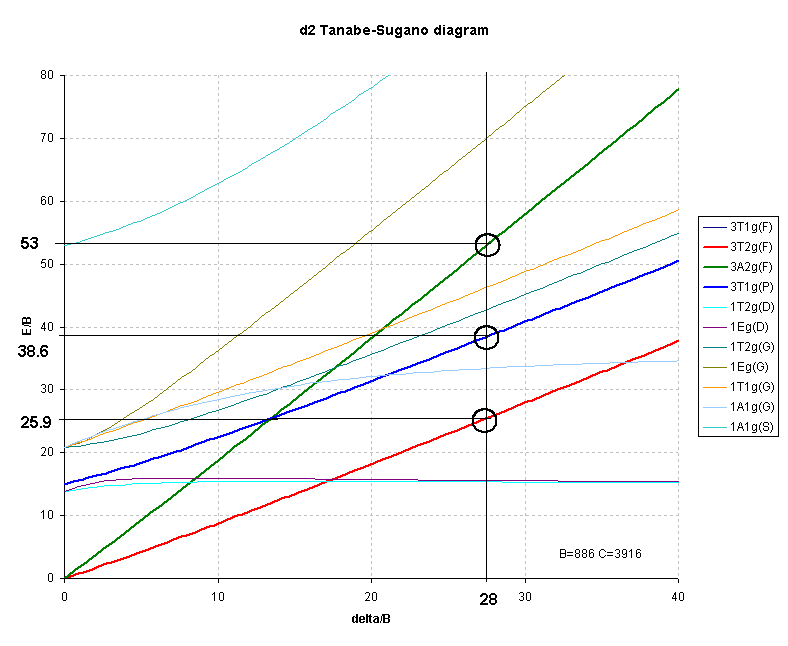
For d² octahedral complexes, few examples have been published. One such is V³⁺ doped in Al₂O₃ where the vanadium ion is generally regarded as octahedral, Table 3.

Table 3. Peak positions for some octahedral V(III) complexes (in cm^-1).
Complex	ν1	ν2	ν3	ν2/ ν1	ν1/ν2	Δ/B	Ref
V³⁺ in Al₂O₃	17400	25200	34500	1.448	0.6906	30.90	13
[VCl₃(MeCN)₃]	14400	21400	?	1.486	0.6729	28.68	4
K₃[VF₆]	14800	23250	?	1.571	0.6365	24.78	4

Interpretation of the spectrum highlights the difficulty of using the right-hand side of the Orgel diagram as previously noted. For d² cases where none of the transitions correspond exactly to Δ often only 2 of the 3 transitions are clearly observed and hence the calculations will have three unknowns (Δ, B and C.I.) but only 2 energies to use in the the analysis.

The first transition can be unambiguously assigned as:

³T_2g ← ³T_1g �� transition energy = 4/5 * Δ + C.I.

But, depending on the size of the ligand field ( Δ) the second transition may be due to:

³A_2g ← ³T_1g �� transition energy = 9/5 * Δ + C.I.

for a weak field or

³T_1g(P) ← ³T_1g �� transition energy = 3/5 * Δ + 15B' + 2 * C.I.

for a strong field.

The transition energies of these terms are clearly different and it is often necessary to calculate (or estimate) values of B, Δ and C.I. for both arrangements and then evaluate the answers to see which fits better.

The difference between the ³A_2g and the ³T_2g (F) lines should give Δ. In this case Δ is equal to either:
25200 - 17400 = 7800 cm^-1
or 34500 - 17400 = 17100 cm^-1.
Given that we expect Δ to be greater than 15000 cm^-1 then we must interpret the second transition as to the ³T_2g(P) and the third to ³A_2g. Further evaluation of the expressions then gives C.I. as 3720 cm^-1 and B' as 567 cm^-1.

Solving the equations like this for the three unknowns can ONLY be done if the three transitions are observed. When only two transitions are observed, a series of equations[14] have been determined that can be used to calculate both B and Δ. This approach still requires some evaluation of the numbers to ensure a valid fit. For this reason, Tanabe-Sugano diagrams become a better method for interpreting spectra of d² octahedral complexes.

Using Tanabe-Sugano diagrams

The use of Orgel diagrams allows a qualitative description of the spin-allowed electronic transitions expected for states derived from D and F ground terms. Only 2 diagrams are needed for high spin d²-d⁹ and both tetrahedral and octahedral ions are covered.

Tanabe-Sugano diagrams were developed in the 1950's to give a semi-quantitative approach and include both high and low spin ions and not only the spin-allowed transitions are shown but the spin-forbidden transitions are displayed as well.

At first glance they can appear quite daunting, but in practice they are much easier to use for interpreting spectra and provide much more information. The obvious differences are the presence of the additional lines and that the ground state is shown as the base line along the X axis rather than as a straight line or curve originating from the Y axis.

On the X axis Δ/B' is plotted while on the Y axis E/B' is plotted, where B' is the modified Racah B parameter that exists in the complex.

A separate diagram is needed for each electronic configuration d²-d⁹ and for the d⁴-d⁷ cases both the high spin and low spin electronic configurations are shown. The high spin is on the left-hand-side of the vertical line on the diagram.

For the d2 case where it is difficult to use an Orgel diagram, the TS diagram is shown below. The ground state is ³T_1g which is plotted along the base line.
Note that the transitions that occur are dependent on the sizes of Δ and B and the A_2g term may be either higher or lower than the T_1g (P) term (depending on whether Δ/B' is greater than about 15).

For the V(III) aqua ion, transitions are observed at 17,200 and 25,600 cm^-1 which are assigned to the 3T_2g ← 3T_1g and 3T_1g(P) ← 3T_1g (F) respectively.
Interpretation requires taking the ratio of these frequencies and then finding the position on the diagram where the height of the 3T_1g(P) / 3T_2g exactly matches that ratio.

For a ratio of 1.49, this is found on the diagram below at Δ/B' of 28.0.

Reading off the position on the Y axis for the three spin-allowed lines gives E/B' values of 25.9, 38.6 and 53 (3T_2g, 3T_1g and 3A_2g)

To determine the value of Δ and B' is now relatively straightforward since from the first transition energy of 17,200 cm^-1 and the value of E/B' of 25.9 we can equate B' as:
B' = 17,200/ 25.9 or B' = 665 cm^-1
Alternatively from the second transition energy of 25,600 cm^-1 and the value of E/B' of 38.6 we can equate B' as:
B' = 25,600/ 38.6 or B' = 663 cm^-1 which is in excellent agreement with the value found from the first transition.

The value of Δ can then be determined from the Δ/B' ratio of 28.0 and the value just calculated for B' of 665 cm^-1.
This gives Δ as 28.0 x 665 = 18,600 cm^-1

The transition ³A_2g ← 3T_1g would be predicted to occur at 53 x 665 that is 35,245 cm^-1 (or 284 nm) which is in the UV region and not observed. (Possibly obscured by charge transfer bands).

The values of Δ and B' can be compared to similar V(III) complexes and it should be noted that in general for M(III) ions the Δ value is often about 3/2 times the value expected for M(II) ions.

The free ion value of B for a V(III) ion is 860 cm^-1 and the reduction of this value noted for the observed B' is a measure of what is described as the Nephelauxetic Effect.

The Nephelauxetic Effect

The Racah repulsion parameters for a metal complex vary as the ligand is changed

As the complex becomes more covalent the electrons are to some extent spread over the ligands so the electron-electron repulsion is reduced
This reduction in repulsion as covalency increases is called the nephelauxetic effect (literally "cloud expanding")

A nephelauxetic series can be set up based on the variation of the Racah parameter.
A large reduction in B (free ion) indicates a strong Nephelauxetic Effect.

{B(free ion)- B'(Complex)} / B(free ion)

The Nephelauxetic Series is given by:

  F- < H₂O < urea < NH₃ < en ~ C₂O₄^2- < NCS- < Cl- ~ CN- < Br- < S^2- ~ I-

This series is consistent with fluoride complexes being the most ionic and giving a small reduction in B while covalently bonded ligands such as I- give a large reduction of B.

N.B. The order of the nephelauxetic series is NOT the same as the spectrochemical series as one is an indication of B and the other of Δ

As an example of a Cr(III) complex, using the observed peaks found for [Cr(NH₃)₆]³⁺ in Table 1 above, namely ν₁ = 21550 cm^-1 and ν₂ = 28500 cm^-1 the ratio of ν₂/ν₁ = 1.32.
The value of Δ is obtained directly from the first transition so Δ/B' is equal to ν₁/B' and finding B' is now relatively straightforward since from the first transition energy of 21,550 cm^-1 and the value of Δ/B' (ν1/B') of 32.6 we get:
B' = 21,550/ 32.6 or B' = 661 cm^-1
The third peak can then be predicted to occur at 69.64 * 661 = 46030 cm^-1 or 217 nm (well in the UV region and probably hidden by charge transfer or solvent bands).

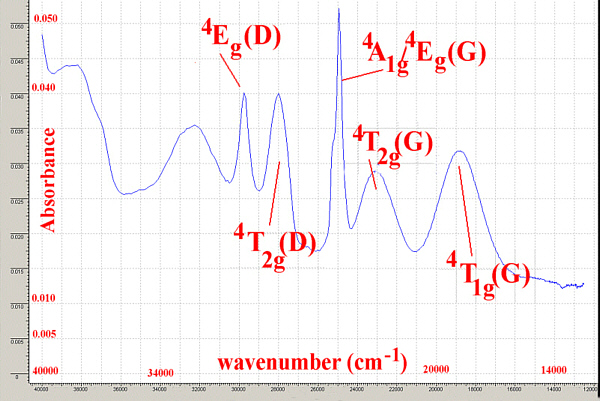
It is important to remember that for spectra recorded in solution the width of the peaks may be as large as 1-2000 cm^-1 so as long as it is possible to unambiguously assign peaks, the techniques are valuable.

high-spin octahedral d⁵ case and low-spin complexes

For Mn(II) and other d⁵ cases, the ground state is ⁶S and higher states include, ⁴G, ⁴D, ⁴P ⁴F etc.
It is expected that since there are NO spin-allowed transitions possible, the electronic spectrum should only contain very weak bands. For the other electronic configurations spin-forbidden bands are rarely observed since they are hidden by the more intense spin-allowed transitions. Since there are now no spin-allowed transitions, by amplifying the signal and using concentrated solutions, a number of weak peaks can be seen.

The Tanabe-Sugano diagram can be used to interpret these bands by once again calculating the ratio of the energies of 2 peaks and finding that position on the diagram.

Use of JAVA applets and spreadsheets

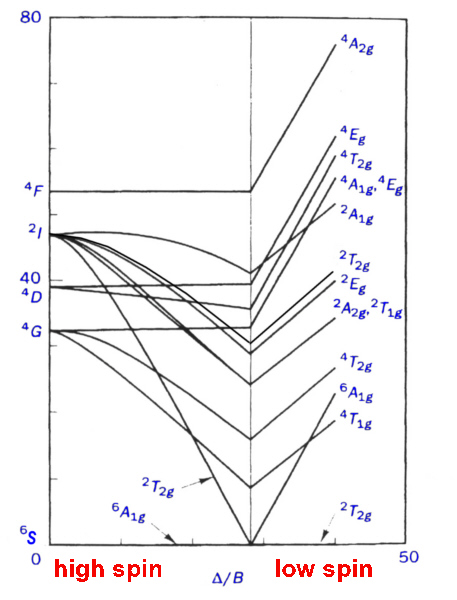
To overcome the problem of small diagrams found in textbooks, it was decided to generate our own Tanabe-Sugano diagrams using spreadsheets. This was done, using the transition energies given in the Appendix, for the spin-allowed transitions and using CAMMAG to generate the energies of the spin-forbidden transitions.

Even so, the method of finding the correct X-intercept is somewhat tedious and time-consuming and a different approach was devised using JAVA applets.

The JAVA applets display the transitions and when the user clicks on any region of the graph then the values of ν₂/ ν₁ and ν₃/ν₁ are displayed. In addition, the values of Δ/B and the Y-intercepts are given as well. This simplifies the process of determining the best fit for Δ/B.

The expected ranges for the ratio of ν₂/ν₁ are:

for d2 (oct) 2.2 - 1.3 for Δ/B 10 - 35
for d3 (oct) 1.8 - 1.2 for Δ/B 0 - 50
for d8 (oct) 1.8 - 1.5 for Δ/B 0 - 18
for d7 (tet) 1.8 - 1.5 for Δ/B 0 - 15

These ratios show the need for a certain degree of precision in attempting to analyse the spectra, especially for d⁷ and d⁸. It has been suggested that instead of using ν₂/ ν₁ that any two ratios can be used and graphs of these plots were produced by Lever in the 1960's[11]. Once again though the published diagrams are rather small and so the spreadsheets above contain these charts which can be printed in larger scale. The slopes of the various ratio lines vary greatly and it is useful to examine the region of interest first before deciding on which set of lines should be used for analysis. If only 2 peaks are observed then this is not an option.

For the spin-allowed diagrams:

The first applies to d3, d8 (oct) d2, d7 (tet) systems.
the second applies to d2, d7 (high spin only) (oct), d3, d8 (tet) systems.

A full set of Tanabe-Sugano diagrams that has both the spin-allowed and spin-forbidden energies are available as well.

Further information for use in laboratory classes is available and some example calculations are available as well.

References

1. Basic Inorganic Chemistry, F.A.Cotton, G.Wilkinson and P.L.Gaus, 3rd edition, John Wiley and Sons, Inc. New York, 1995.
2. Physical Inorganic Chemistry, S.F.A.Kettle, Oxford University Press, New York, 1998.
3. Complexes and First-Row Transition Elements, D.Nicholls, Macmillan Press Ltd, London 1971.
4. The Chemistry of the Elements, N.N.Greenwood and A.Earnshaw, Pergamon Press, Oxford, 1984.
5. Concepts and Models of Inorganic Chemistry, B.E.Douglas, D.H.McDaniel and J.J.Alexander 2nd edition, John Wiley & Sons, New York, 1983.
6. Inorganic Chemistry, J.A.Huheey, 3rd edition, Harper & Row, New York, 1983.
7. Inorganic Chemistry, G.L.Meissler and D.A.Tarr, 2nd edition, Prentice Hall, New Jersey, 1998.
8. Inorganic Chemistry, D.F.Shriver and P.W.Atkins, 3rd edition, W.H.Freeman, New York, 1999.
9. Basic Principles of Ligand Field Theory, H.L.Schlafer and G.Gliemann, Wiley-Interscience, New York, 1969.
10. Y.Tanabe and S.Sugano, J. Phys. Soc. Japan, 9, 1954, 753 and 766.
11(a). Inorganic Electronic Spectroscopy, A.B.P.Lever, 2nd Edition, Elsevier Publishing Co., Amsterdam, 1984.
11(b). A.B.P.Lever in Werner Centennial, Adv. in Chem Series, 62, 1967, Chapter 29, 430.
12(a). Introduction to Ligand Fields, B.N.Figgis, Wiley, New York, 1966.
12(b). Ligand Field Theory and Its Applications, B.N. Figgis and M.A. Hitchman, Wiley-VCH: New York, 2000. ISBN 0-471-31776-4.
13. E.Konig, Structure and Bonding, 9, 1971, 175.
14. Y. Dou, J. Chem. Educ, 67, 1990, 134.

Appendix

Transitions calculated for spin-allowed terms in the Tanabe-Sugano diagrams.

Octahedral d³ (e.g. Chromium(III) ).

⁴T_2g ← ⁴A_2g , ν₁/B= Δ/B

⁴T_1g(F) ← ⁴A_2g, ν₂/B= ½{15 + 3( Δ/B) - √(225 - 18(Δ/B) + ( Δ/B)² ) }

⁴T_1g(P) ← ⁴A_2g, ν₃/B= ½{15 + 3( Δ/B) + √(225 - 18(Δ/B) + ( Δ/B)² ) }

from this, the ratio ν₂/ν₁ would become:

½{15 + 3( Δ/B) - √(225 - 18(Δ/B) + ( Δ/B)² ) } / Δ/B

and the range of Δ/B required is from ~15 to ~55

Octahedral d⁸ (e.g. Nickel(II) ).

³T_2g ← ³A_2g, ν1/B= Δ/B

³T_1g(F) ← ³A_2g, ν2/B= ½{15 + 3(Δ/B) - √(225 - 18(Δ/B) + ( Δ/B)² ) }

³T_1g(P) ← ³A_2g, ν3/B= ½{15 + 3(Δ/B) + √(225 - 18(Δ/B) + ( Δ/B)² ) }

from this the ratio ν₂/ν₁ would become:

½{15 + 3( Δ/B) - √(225 - 18(Δ/B) + ( Δ/B)² ) } / Δ/B

and the range of Δ/B required is from ~5 to ~17

Octahedral d² (e.g. Vanadium(III) ).

³T_2g ← ³T_1g , ν1/B= ½{(Δ/B) - 15 + √(225 + 18(Δ/B) + ( Δ/B)² ) }

³T_1g(P) ← ³T_1g, ν2/B= √(225 + 18(Δ/B) + (Δ/B)² )

³A_2g ← ³T_1g, ν3/B= ½{ 3 (Δ/B) -15 + √(225 + 18(Δ/B) + ( Δ/B)² ) }

from this the ratio ν₂/ν₁ would become:

√(225 + 18(Δ/B) + ( Δ/B)² ) / ½{( Δ/B) - 15 + √(225 + 18(Δ/B) + ( Δ/B)² ) }

and the range of Δ/B required is from ~15 to ~35

Tetrahedral d⁷ (e.g. Cobalt(II) ).

⁴T₂ ← ⁴A₂, ν1/B= Δ/B

⁴T₁ (F) ← ⁴A₂, ν2/B= ½{15 + 3(Δ/B) - √(225 - 18(Δ/B) + ( Δ/B)² ) }

⁴T₁ (P) ← ⁴A₂, ν3/B= ½{15 + 3(Δ/B) + √(225 - 18(Δ/B) + ( Δ/B)² ) }

from this the ratio ν₂/ν₁ would become:

½{15 + 3(Δ/B) - √(225 - 18( Δ/B) + ( Δ/B)² ) } / Δ/B

and the range of Δ/B required is from ~3 to ~8.

Acknowledgments

Thanks are due to Christopher Muir, for help with developing the JAVA applets.

return to the CHEM2101 (C21J) course outline

Return to Chemistry, UWI-Mona, Home Page

Created and maintained by Prof. Robert J. Lancashire
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica.

Created Feb 1999. Links checked and/or last modified 28th March 2011.
URL http://wwwchem.uwimona.edu.jm/courses/C21Jspec_TS.html